Rätselsammlung: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „bla“ |
Keine Bearbeitungszusammenfassung |
||
| (93 dazwischenliegende Versionen von 6 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Bestätigt}} | |||
Hier findet ihr eine Sammlung an Rätseln, die ihr in euren Abenteuern verbauen könnt. Die meisten Rätsel sind so offen gehalten, dass sie entsprechend immer auf das eigene Abenteuer anpassbar sind. Wenn ihr weitere Rätsel habt, fügt sie gerne unten ein. | |||
==Worträtsel== | |||
Worträtsel beinhalten all diejenigen Rätsel, die zum Ziel haben ein einziges Wort oder einen Begriff herauszufinden. | |||
===Was bin ich - Sarg === | |||
{{dia|Rätsel:Der es macht, der will es nicht; | |||
der es trägt, behält es nicht; | |||
der es kauft, der braucht es nicht; | |||
der es hat, der weiß es nicht. | |||
Wer bin ich?}} | |||
{{spoiler|Lösung:|Der Sarg}} | |||
===Was bin ich - Geheimnis === | |||
{{dia|Rätsel:Wenn du mich hast, willst du mich weitergeben. | |||
Wenn du mich weitergibst, bin ich nicht mehr ich. | |||
Was bin ich?}} | |||
{{spoiler|Lösung:| Das Geheimnis}} | |||
===Was bin ich - Nase=== | |||
{{dia|Rätsel:Ich habe zwei Flügel, kann aber nicht fliegen. | |||
Ich kann laufen, jedoch aber nicht gehen. | |||
Ich habe ein Bein, aber kann nicht stehen. | |||
Ich trage eine Brille tragen, aber kann nicht sehen. | |||
Wer bin ich?}} | |||
{{spoiler|Lösung:|Die Nase}} | |||
==Mathematische Rätsel== | |||
Mathematische Rätsel umfassen alles, was direkte Mathematik benötigt, so wie Zahlenrätsel, Rechenrätsel, etc. | |||
===Meine Schwester ist doppelt so alt=== | |||
Die Zahlen können variieren, nur die Lösung muss dementsprechend angepasst werden. | |||
{{box|Ich bin 15 Jahre alt und meine Schwester ist doppelt so alt wie Ich. Wie alt wäre Ich, wenn sie 68 Jahre alt wäre?}} | |||
{{spoiler|Lösung| | |||
Die Differenz zwischen den Schwestern ist 15 Jahre. Wenn die Schwester 68 Jahre alt ist, bleibt die Differenz von 15 Jahren. Ich wäre also 53 Jahre alt.}} | |||
===Zahlenkette=== | |||
Es werden immer Zahlen in einer Reihe aufgezählt und es muss die letzte Zahl ergänzt werden. Wie die Reihe aufgebaut ist, kann ganz unterschiedlich sein. Auch die Komplexität kann hier variieren. Hier sind ein paar Beispiele: | |||
{{box|Beispiel1 - einfach: | |||
1 4 9 16 25 ???}} | |||
{{spoiler|Lösung|36 - Immer 1<big>2</big>, 2<big>2</big>... und 6<big>2</big>}} | |||
{{box|Beispiel2 - mittel: | |||
1 4 9 16 25 ???}} | |||
{{spoiler|Lösung|36 - Immer 1<big>2</big>, 2<big>2</big>... und 6<big>2</big>}} | |||
{{box|Beispiel3 - schwer: | |||
27 88 271 820 2467 ???}} | |||
{{spoiler|Lösung|7408 - Immer die vorige Zahl * 3 und +7 rechnen.}} | |||
==Chiffre== | |||
Chiffre sind Verschlüsselungsverfahren von meist Texten, die die Spieler entschlüsseln müssen um an Informationen zu gelangen. | |||
===Caeser Verfahren=== | |||
Es gibt beim Verfahren verschiedene sogenannte Schlüssel. Mit diesen Schlüsseln lassen sich verschiedene Buchstaben kodieren. | |||
{{box|Z.B wird beim Schlüssel 3 der Buchstabe A zum Buchstaben D. Oder beim Schlüssel 1 wird der Buchstabe A zu B.}} | |||
Je nach Nummer der Schlüssel wird der entsprechende Buchstabe mit dem ensprechenden Buchstaben an der angegebene Stelle (hier 3 von A), vom Ausgangspunkt des jeweilig zu entschlüsselnden Buchstaben, ersetzt. Wenn man bei einem Buchstaben höher als bei Z ist fängt man wieder bei A an. | |||
Das System wird einfach ersichtlich, wenn man den Buchstaben Zahlen zuordnet. Dies könnte für eine weitere Rätselmöglichkeit sorgen, wenn man es entsprechend vorbereitet. Normalerweise fängt man bei A und 1 an bis Z 26, dann ist erkennbar um wie viel die Buchstaben verschoben sind. | |||
{{bsp|Klartext: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | |||
Geheim: H I J K L M N O P Q R S T U V W X Y Z A B C D E F G}} | |||
===Textstellenverschlüsslung=== | |||
==Logikrätsel== | |||
Welchen Hut hab ich auf | |||
=== Huträtsel === | |||
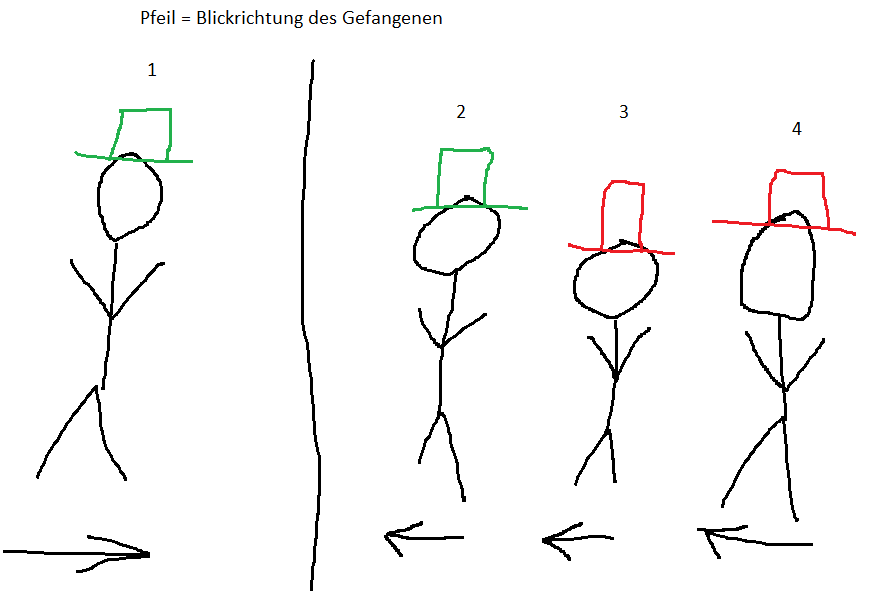
{{box|Vier Gefangene sitzen in je einer Zelle und sind dort angekettet. Einer der Gefangenen sitzt hinter einer Wand und kann nicht gesehen werden. Die anderen drei sind in einer Linie aufgestellt, sodass sie nur die Gefangenen vor sich erkennen können. (s. Skizze). Die Nummern in dieser Skizze sind die Nummern der Gefangenen. Die Gefangenen wissen, dass jeder von ihnen einen Hut trägt und dass 2 der vier Hüte rot sind und dass die anderen 2 grün sind. Kein Gefangener kann seine Blickrichtung ändern oder seine Position verlassen. Keiner der Gefangenen weiß welchen Hut er selbst trägt. Sobald einer der Gefangenen in der Lage ist zu sagen welchen Hut er selbst trägt, werden alle freigelassen. }} | |||
{{bildklein|Hut-Rätzel - Skizze.png|Skizze des Huträtsels}} | |||
Welche Gefangener ist in der Lage zu sagen welchen Hut er trägt? | |||
{{spoiler|Lösung:|Gefangener Nummer 3{{br}} Der Gefangene Nummer 4 sieht, dass die beiden Gefangenen vor ihm verschiedene Hüte tragen. Da er nicht weiß welchen Hut der Gefangene Nummer 1 hat, kann er nicht sagen welchen Hut er selbst trägt und schweigt. Da Gefangener Nummer 3 hört, dass Gefangener Nummer 4 nichts sagt, kann er schlussfolgern, dass dieser nicht weiß welchen Hut er selbst trägt. Dies kann nur der Fall sein, wenn Gefangener Nummer 2 und 3 verschiedene Hüte tragen. Gefangener Nummer 3 sieht welchen Hut Gefangener Nummer 2 trägt und weiß, daher, dass er selbst den andersfarbigen trägt.}} | |||
===Zwei Wachen einer lügt=== | |||
{{box|Zwei Personen stehen zwei Türen. Euer Ziel ist es herauszufinden, welche die Tür ist, durch die ihr müsst. Eine der Personen lügt allerdings immer, während die andere immer die Wahrheit sagt. Welche Frage stellt ihr um die Antwort herauszufinden?}} | |||
{{spoiler|Lösung|"Wenn ich die andere Person fragen würde, welche Tür die richtige wäre, welche Antwort würde sie mir geben?" Egal welche der beiden Personen du fragst, sie wird immer die falsche Tür nennen, somit weißt du, dass die Andere dementsprechend die Richtige ist.}} | |||
===simple nim=== | |||
Dieses Rätsel wird normalerweise gegen einen NPC gespielt. Es werden 13 Münzen auf den Tisch gelegt, die Spieler ziehen abwechselnd 1 bis 3 Münzen. Die Person, die die letzte Münze nimmt hat verloren. | |||
{{spoiler|Lösung: | |||
|Die Prämisse ist, dass nim ein Spiel ist, welches der Gegenspieler immer gewinnt. Der Spielleiter bringt den Spieler dazu anzufangen und füllt seinen Zug immer auf 4 auf (nimmt der Spieler 1, nimmt der Master 3; nimmt der Spieler 2, nimmt der Master 2; nimmt der Spieler 3, nimmt der Master 1). Dadurch muss der Spieler automatisch immer die letzte Münze nehmen und hat immer gewonnen}} | |||
===nim=== | |||
===Wolf Ziege Kohl=== | |||
{{box|Ein Bauer hat einen Wolf, eine Ziege und einen Kohlkopf, die er über einen Fluss bringen will. Er hat dazu ein Boot, auf dem er immer maximal 2 von seinen Besitztümern mitnehmen kann. Lässt er die Ziege und den Wolf allerdings allein, isst der Wolf die Ziege, lässt er Ziege und Kohl allein, isst die Ziege den Kohl}} | |||
{{spoiler|Lösung| | |||
{{Kohlrätsel}} | |||
}} | |||
===Personen überqueren eine Brücke=== | |||
{{box|Vier Personen wollen bei Nacht eine Brücke überqueren. Das geht allerdings nur im Licht einer Laterne, da es dank der Dunkelheit sonst unmöglich ist. | |||
Die Laterne hat allerdings nur eine begrenzte Brenndauer und der Lichtkegel Platz für zwei Personen, somit muss also eine efektive Lösung gefunden werden.}} | |||
{|class="wikitable" | |||
!Person | |||
! Dauer zum überlaufen | |||
|- | |||
|A | |||
|5 | |||
|- | |||
|B | |||
|10 | |||
|- | |||
|C | |||
|20 | |||
|- | |||
|D | |||
|25 | |||
|- | |||
|} | |||
<big>'''Die Lösung ist nur dann richtig, wenn die kürzeste Zeit erreicht wurde'''</big> | |||
{{spoiler|Lösung|A und B überqueren die Brücke, A kehrt mit der Laterne zurück. Anschließend gehen C und D als die beiden langsamsten gemeinsam hinüber, die Laterne bringt B zurück, bevor er zusammen mit A die Brücke ein weiteres Mal überquert. Dieser Plan benötigt nur 10 + 5 + 25 + 10 + 10 {{=}} 60 Minuten. | |||
}} | |||
===3 Löwe, 3 Büffel=== | |||
{{box|In der Savanna befinden sich 3 Büffel und 3 Löwen, die einen Fluss überqueren wollen. Dazu steht ihnen ein Boot zur Verfügung, welches maximal 2 Tiere transprtieren kann und nicht leer reisen kann. Nun begibt es sich aber, dass die Löwen, sollten sie auf einer Seite in der Überzahl sein, die Büffel fressen. Schafft ihr es die komplette Gruppe über den Fluss zu bekommen, ohne, dass jemand gefressen wird?}} | |||
{{spoiler|Lösung| | |||
{{Löwenrätsel}} | |||
}} | |||
==Visuelle Rätsel== | |||
Visuelle Rästel umfassen alle Rätsel, die hauptsächlich darauf basieren, dass die Spieler ein Bild vor sich liegen haben. | |||
===9 Punkte 4 Linien=== | |||
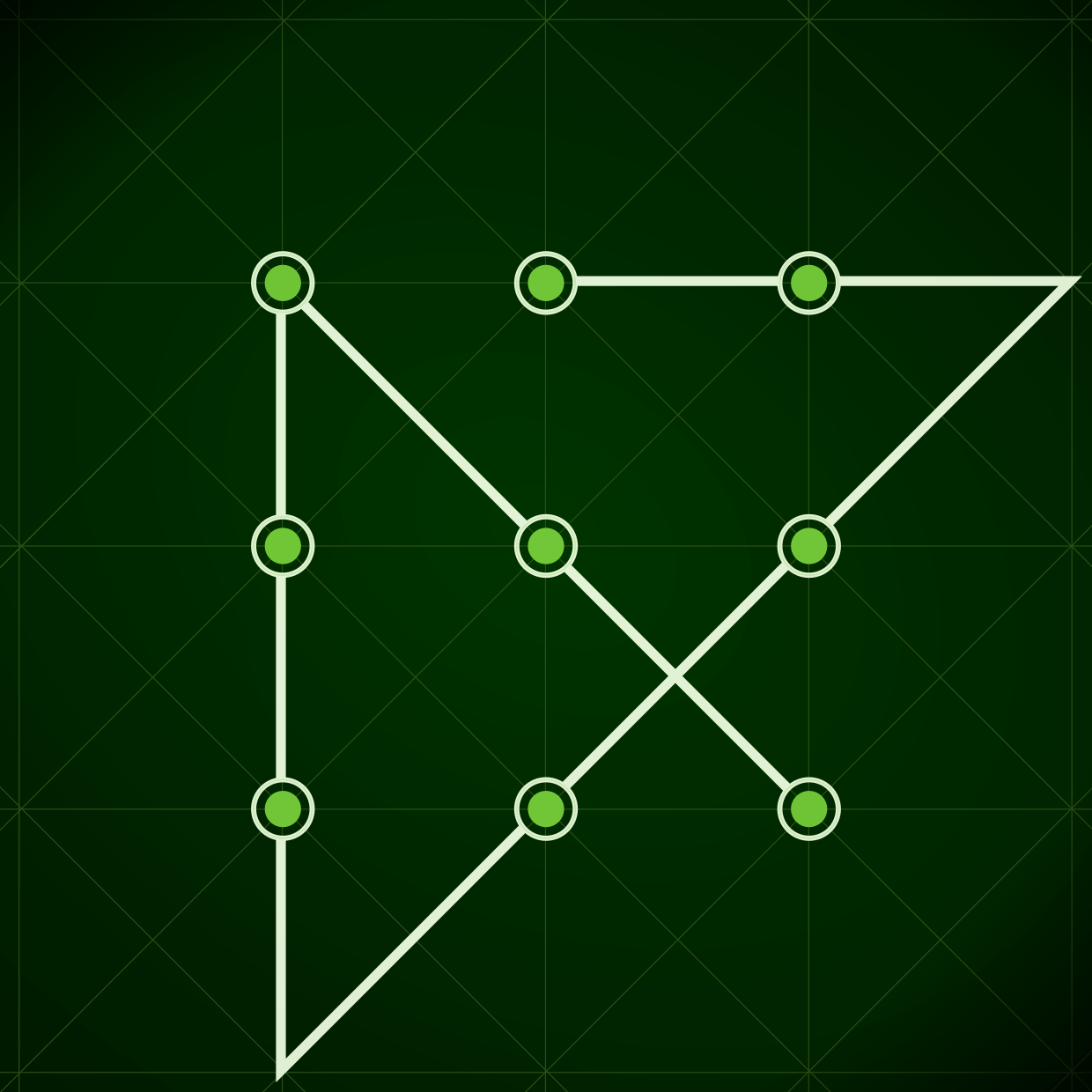
Verbinde 9 Punkte, die in einem 3x3 Feld angeordnet sind mit 4 geraden Linien, ohne den Stift abzusetzen. | |||
{{bildklein|Dysnomia Rätsel.png}} | |||
{{spoiler|Lösung | |||
|{{bildklein|Dysnomia Rätsel Lösung.png}} | |||
}} | |||
==Gruppenrätsel== | |||
Gruppenrätsel zeichnen sich damit aus, dass verschiedene Teile der Gruppe, verschiedene Informationen oder Mittel erhalten und sich so absprechen müssen, dass sie gemeinsam das Rätsel lösen können. | |||
==Praktische Rätsel== | |||
Praktische Rätschel beschreiben alle Rätsel, welche die Spieler aktiv mit irgendetwas Physischen interagieren lassen. Das kann auch durch ein Computerprogramm geschehen, allerdings ist der entscheidende Teil, dass die Spieler das vor ihnen befindliche aktiv verändern um zu einer Lösung zu finden. | |||
===Streichhölzer=== | |||
===Schafe einzeunen=== | |||
==Kompetetive Rätsel (PvP)== | |||
Kompetitive Rätsel beruhen auf dem Prinzip der gegenseitigen Herausforderung, sprich, Spieler gegen Spieler. | |||
=== Bild(er)raten === | |||
Die Spieler bekommen Stückweise ein Bild gezeigt. Je nach Variante wird dieses entweder mit der Zeit immer schärfer, wird erst fertig gemalt (immer mehr Elemente hinzugefügt) oder Stückweise aufgedeckt. | |||
Wer zuerst errät worum es sich handelt hat gewonnen. Wer falsch rät hat verloren. | |||
[[Kategorie:Tipps und Tricks]] | |||
Aktuelle Version vom 22. August 2025, 19:49 Uhr

Hier findet ihr eine Sammlung an Rätseln, die ihr in euren Abenteuern verbauen könnt. Die meisten Rätsel sind so offen gehalten, dass sie entsprechend immer auf das eigene Abenteuer anpassbar sind. Wenn ihr weitere Rätsel habt, fügt sie gerne unten ein.
Worträtsel
Worträtsel beinhalten all diejenigen Rätsel, die zum Ziel haben ein einziges Wort oder einen Begriff herauszufinden.
Was bin ich - Sarg
|
Rätsel: „Der es macht, der will es nicht; der es trägt, behält es nicht; der es kauft, der braucht es nicht; der es hat, der weiß es nicht. Wer bin ich?“ |
| Lösung: |
|---|
| Der Sarg |
Was bin ich - Geheimnis
|
Rätsel: „Wenn du mich hast, willst du mich weitergeben. Wenn du mich weitergibst, bin ich nicht mehr ich. Was bin ich?“ |
| Lösung: |
|---|
| Das Geheimnis |
Was bin ich - Nase
|
Rätsel: „Ich habe zwei Flügel, kann aber nicht fliegen. Ich kann laufen, jedoch aber nicht gehen. Ich habe ein Bein, aber kann nicht stehen. Ich trage eine Brille tragen, aber kann nicht sehen. Wer bin ich?“ |
| Lösung: |
|---|
| Die Nase |
Mathematische Rätsel
Mathematische Rätsel umfassen alles, was direkte Mathematik benötigt, so wie Zahlenrätsel, Rechenrätsel, etc.
Meine Schwester ist doppelt so alt
Die Zahlen können variieren, nur die Lösung muss dementsprechend angepasst werden.
Ich bin 15 Jahre alt und meine Schwester ist doppelt so alt wie Ich. Wie alt wäre Ich, wenn sie 68 Jahre alt wäre?
| Lösung |
|---|
|
Die Differenz zwischen den Schwestern ist 15 Jahre. Wenn die Schwester 68 Jahre alt ist, bleibt die Differenz von 15 Jahren. Ich wäre also 53 Jahre alt. |
Zahlenkette
Es werden immer Zahlen in einer Reihe aufgezählt und es muss die letzte Zahl ergänzt werden. Wie die Reihe aufgebaut ist, kann ganz unterschiedlich sein. Auch die Komplexität kann hier variieren. Hier sind ein paar Beispiele:
Beispiel1 - einfach: 1 4 9 16 25 ???
| Lösung |
|---|
| 36 - Immer 12, 22... und 62 |
Beispiel2 - mittel: 1 4 9 16 25 ???
| Lösung |
|---|
| 36 - Immer 12, 22... und 62 |
Beispiel3 - schwer: 27 88 271 820 2467 ???
| Lösung |
|---|
| 7408 - Immer die vorige Zahl * 3 und +7 rechnen. |
Chiffre
Chiffre sind Verschlüsselungsverfahren von meist Texten, die die Spieler entschlüsseln müssen um an Informationen zu gelangen.
Caeser Verfahren
Es gibt beim Verfahren verschiedene sogenannte Schlüssel. Mit diesen Schlüsseln lassen sich verschiedene Buchstaben kodieren.
Z.B wird beim Schlüssel 3 der Buchstabe A zum Buchstaben D. Oder beim Schlüssel 1 wird der Buchstabe A zu B.
Je nach Nummer der Schlüssel wird der entsprechende Buchstabe mit dem ensprechenden Buchstaben an der angegebene Stelle (hier 3 von A), vom Ausgangspunkt des jeweilig zu entschlüsselnden Buchstaben, ersetzt. Wenn man bei einem Buchstaben höher als bei Z ist fängt man wieder bei A an.
Das System wird einfach ersichtlich, wenn man den Buchstaben Zahlen zuordnet. Dies könnte für eine weitere Rätselmöglichkeit sorgen, wenn man es entsprechend vorbereitet. Normalerweise fängt man bei A und 1 an bis Z 26, dann ist erkennbar um wie viel die Buchstaben verschoben sind.
Beispiel:
| Klartext: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Geheim: H I J K L M N O P Q R S T U V W X Y Z A B C D E F G |
Textstellenverschlüsslung
Logikrätsel
Welchen Hut hab ich auf
Huträtsel
Vier Gefangene sitzen in je einer Zelle und sind dort angekettet. Einer der Gefangenen sitzt hinter einer Wand und kann nicht gesehen werden. Die anderen drei sind in einer Linie aufgestellt, sodass sie nur die Gefangenen vor sich erkennen können. (s. Skizze). Die Nummern in dieser Skizze sind die Nummern der Gefangenen. Die Gefangenen wissen, dass jeder von ihnen einen Hut trägt und dass 2 der vier Hüte rot sind und dass die anderen 2 grün sind. Kein Gefangener kann seine Blickrichtung ändern oder seine Position verlassen. Keiner der Gefangenen weiß welchen Hut er selbst trägt. Sobald einer der Gefangenen in der Lage ist zu sagen welchen Hut er selbst trägt, werden alle freigelassen.
| Skizze des Huträtsels |
Welche Gefangener ist in der Lage zu sagen welchen Hut er trägt?
| Lösung: |
|---|
| Gefangener Nummer 3 Der Gefangene Nummer 4 sieht, dass die beiden Gefangenen vor ihm verschiedene Hüte tragen. Da er nicht weiß welchen Hut der Gefangene Nummer 1 hat, kann er nicht sagen welchen Hut er selbst trägt und schweigt. Da Gefangener Nummer 3 hört, dass Gefangener Nummer 4 nichts sagt, kann er schlussfolgern, dass dieser nicht weiß welchen Hut er selbst trägt. Dies kann nur der Fall sein, wenn Gefangener Nummer 2 und 3 verschiedene Hüte tragen. Gefangener Nummer 3 sieht welchen Hut Gefangener Nummer 2 trägt und weiß, daher, dass er selbst den andersfarbigen trägt. |
Zwei Wachen einer lügt
Zwei Personen stehen zwei Türen. Euer Ziel ist es herauszufinden, welche die Tür ist, durch die ihr müsst. Eine der Personen lügt allerdings immer, während die andere immer die Wahrheit sagt. Welche Frage stellt ihr um die Antwort herauszufinden?
| Lösung |
|---|
| "Wenn ich die andere Person fragen würde, welche Tür die richtige wäre, welche Antwort würde sie mir geben?" Egal welche der beiden Personen du fragst, sie wird immer die falsche Tür nennen, somit weißt du, dass die Andere dementsprechend die Richtige ist. |
simple nim
Dieses Rätsel wird normalerweise gegen einen NPC gespielt. Es werden 13 Münzen auf den Tisch gelegt, die Spieler ziehen abwechselnd 1 bis 3 Münzen. Die Person, die die letzte Münze nimmt hat verloren.
| Lösung: |
|---|
| Die Prämisse ist, dass nim ein Spiel ist, welches der Gegenspieler immer gewinnt. Der Spielleiter bringt den Spieler dazu anzufangen und füllt seinen Zug immer auf 4 auf (nimmt der Spieler 1, nimmt der Master 3; nimmt der Spieler 2, nimmt der Master 2; nimmt der Spieler 3, nimmt der Master 1). Dadurch muss der Spieler automatisch immer die letzte Münze nehmen und hat immer gewonnen |
nim
Wolf Ziege Kohl
Ein Bauer hat einen Wolf, eine Ziege und einen Kohlkopf, die er über einen Fluss bringen will. Er hat dazu ein Boot, auf dem er immer maximal 2 von seinen Besitztümern mitnehmen kann. Lässt er die Ziege und den Wolf allerdings allein, isst der Wolf die Ziege, lässt er Ziege und Kohl allein, isst die Ziege den Kohl
| Lösung | ||||||||
|---|---|---|---|---|---|---|---|---|
|
Personen überqueren eine Brücke
Vier Personen wollen bei Nacht eine Brücke überqueren. Das geht allerdings nur im Licht einer Laterne, da es dank der Dunkelheit sonst unmöglich ist. Die Laterne hat allerdings nur eine begrenzte Brenndauer und der Lichtkegel Platz für zwei Personen, somit muss also eine efektive Lösung gefunden werden.
| Person | Dauer zum überlaufen |
|---|---|
| A | 5 |
| B | 10 |
| C | 20 |
| D | 25 |
Die Lösung ist nur dann richtig, wenn die kürzeste Zeit erreicht wurde
| Lösung |
|---|
| A und B überqueren die Brücke, A kehrt mit der Laterne zurück. Anschließend gehen C und D als die beiden langsamsten gemeinsam hinüber, die Laterne bringt B zurück, bevor er zusammen mit A die Brücke ein weiteres Mal überquert. Dieser Plan benötigt nur 10 + 5 + 25 + 10 + 10 = 60 Minuten. |
3 Löwe, 3 Büffel
In der Savanna befinden sich 3 Büffel und 3 Löwen, die einen Fluss überqueren wollen. Dazu steht ihnen ein Boot zur Verfügung, welches maximal 2 Tiere transprtieren kann und nicht leer reisen kann. Nun begibt es sich aber, dass die Löwen, sollten sie auf einer Seite in der Überzahl sein, die Büffel fressen. Schafft ihr es die komplette Gruppe über den Fluss zu bekommen, ohne, dass jemand gefressen wird?
| Lösung | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Visuelle Rätsel
Visuelle Rästel umfassen alle Rätsel, die hauptsächlich darauf basieren, dass die Spieler ein Bild vor sich liegen haben.
9 Punkte 4 Linien
Verbinde 9 Punkte, die in einem 3x3 Feld angeordnet sind mit 4 geraden Linien, ohne den Stift abzusetzen.
| Lösung | ||
|---|---|---|
|
|
Gruppenrätsel
Gruppenrätsel zeichnen sich damit aus, dass verschiedene Teile der Gruppe, verschiedene Informationen oder Mittel erhalten und sich so absprechen müssen, dass sie gemeinsam das Rätsel lösen können.
Praktische Rätsel
Praktische Rätschel beschreiben alle Rätsel, welche die Spieler aktiv mit irgendetwas Physischen interagieren lassen. Das kann auch durch ein Computerprogramm geschehen, allerdings ist der entscheidende Teil, dass die Spieler das vor ihnen befindliche aktiv verändern um zu einer Lösung zu finden.
Streichhölzer
Schafe einzeunen
Kompetetive Rätsel (PvP)
Kompetitive Rätsel beruhen auf dem Prinzip der gegenseitigen Herausforderung, sprich, Spieler gegen Spieler.
Bild(er)raten
Die Spieler bekommen Stückweise ein Bild gezeigt. Je nach Variante wird dieses entweder mit der Zeit immer schärfer, wird erst fertig gemalt (immer mehr Elemente hinzugefügt) oder Stückweise aufgedeckt.
Wer zuerst errät worum es sich handelt hat gewonnen. Wer falsch rät hat verloren.